| Więcej informacji kliknij na poszczególne punkty | ||||||||||||||||
| 1. Obliczenie długości boków trójkata znając współrzędne punktu w układzie współrzędnych | ||||||||||||||||
| Punkt A | xA | yA | Długość boku AB | |||||||||||||
| 1 | 2 | 3,61 | ||||||||||||||
| Punkt B | xB | yB | Długość boku BC | |||||||||||||
| 3 | -1 | 4,12 | ||||||||||||||
| Punkt C | xC | yC | Długość boku AC | |||||||||||||
| 2 | 3 | 1,41 | ||||||||||||||
| 2. Trójkąt można zbudować jeżeli BC-AC<AB<BC+AC | ||||||||||||||||
| jest taki trójkąt | ||||||||||||||||
| 3. Obliczenie pola trójkata ze wzoru Herona | ||||||||||||||||
| 2,5 | ||||||||||||||||
| 4. Obliczenie pola okręgu opisanego na tym trójkącie | ||||||||||||||||
| 13,88 | ||||||||||||||||
| 5. Obliczyć pole okręgu wpisanego w ten trójkat | ||||||||||||||||
| 0,94 | ||||||||||||||||
| 6. Promień okręgu wpisanego w trójkąt | ||||||||||||||||
| 0,55 | ||||||||||||||||
| 7. Obliczenie promienia okręgu opisanego na tym trójkącie | ||||||||||||||||
| 2,10 | ||||||||||||||||
| 8. Obliczenie katów z twierdzenia cosinusów | ||||||||||||||||
| 0,9417 | -0,1961 | 0,5145 | ||||||||||||||
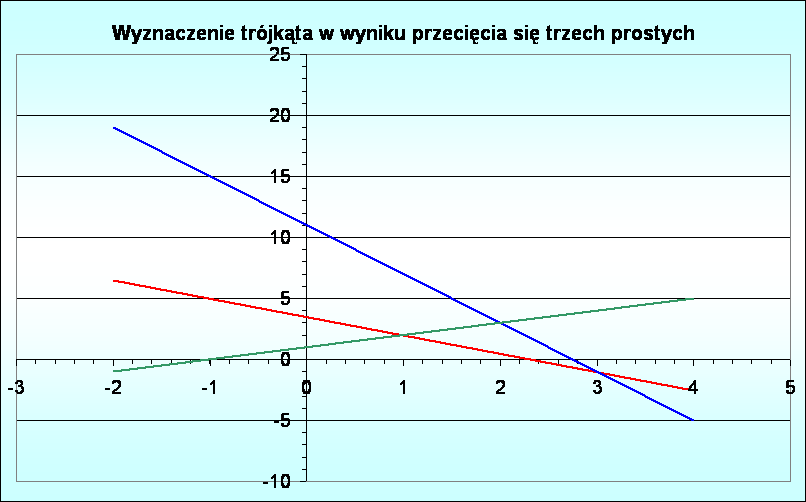
| 9. Narysować powstały trókąt | ||||||||||||||||
| x | y=(yb-ya)/(xb-xa)(x-xa)+ya - ogólny wzór funkcji | |||||||||||||||
| 4 | -2,5 | -5 | 5 | |||||||||||||
| -2 | 6,5 | 19 | -1 | |||||||||||||

|
||||||||||||||||